상세 컨텐츠
본문
오늘도 Manim을 활용해서 일반물리학 연습문제를 풀어보겠습니다. 단원은 벡터와 이차원 운동입니다. 그럼 시작해 볼까요
문제

문제를 읽어보고 문제의 상황을
이해해 봅시다.
수평 즉 지면 기준 30º의 투사각으로
발사된 포물체가 4초 뒤에 산중턱에 정지한 상황입니다.
주어진 물리량들을 정리해볼까요?
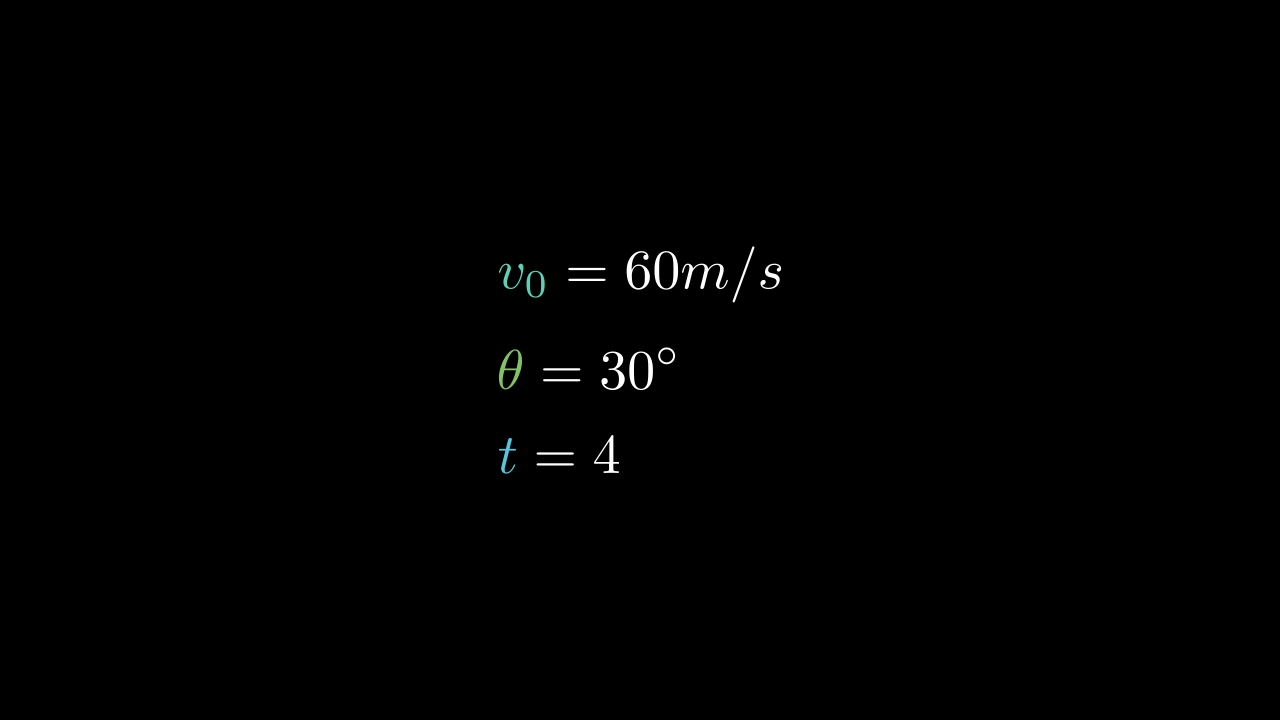
초기속도, 투사각, 정지할 때 까지 걸린 시간
이 세가지 물리량이 문제에서 주어졌습니다.
그러면 문제 상황을 그림으로
확인해 보겠습니다.
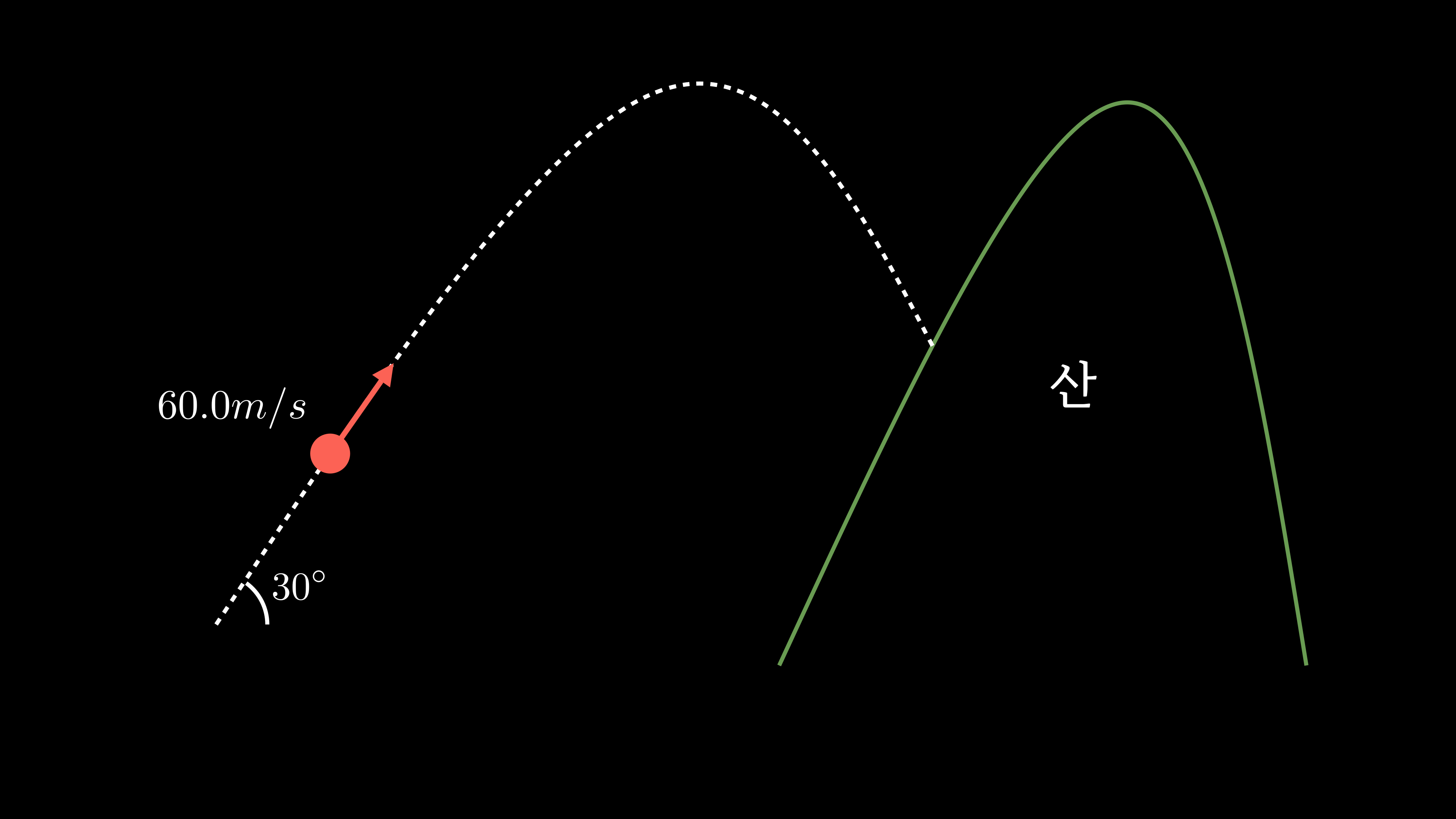
포물체가 포물선을 따라 초기 속도 60.0m/s
투사각 30도의 조건으로 포물선 운동하는 상황입니다.
애니메이션으로 확인해 볼까요?
포물체의 운동을 애니메이션으로
확인해 보았습니다.
그럼 궤적의 최고점에서 포물체의
속도를 구해볼까요?
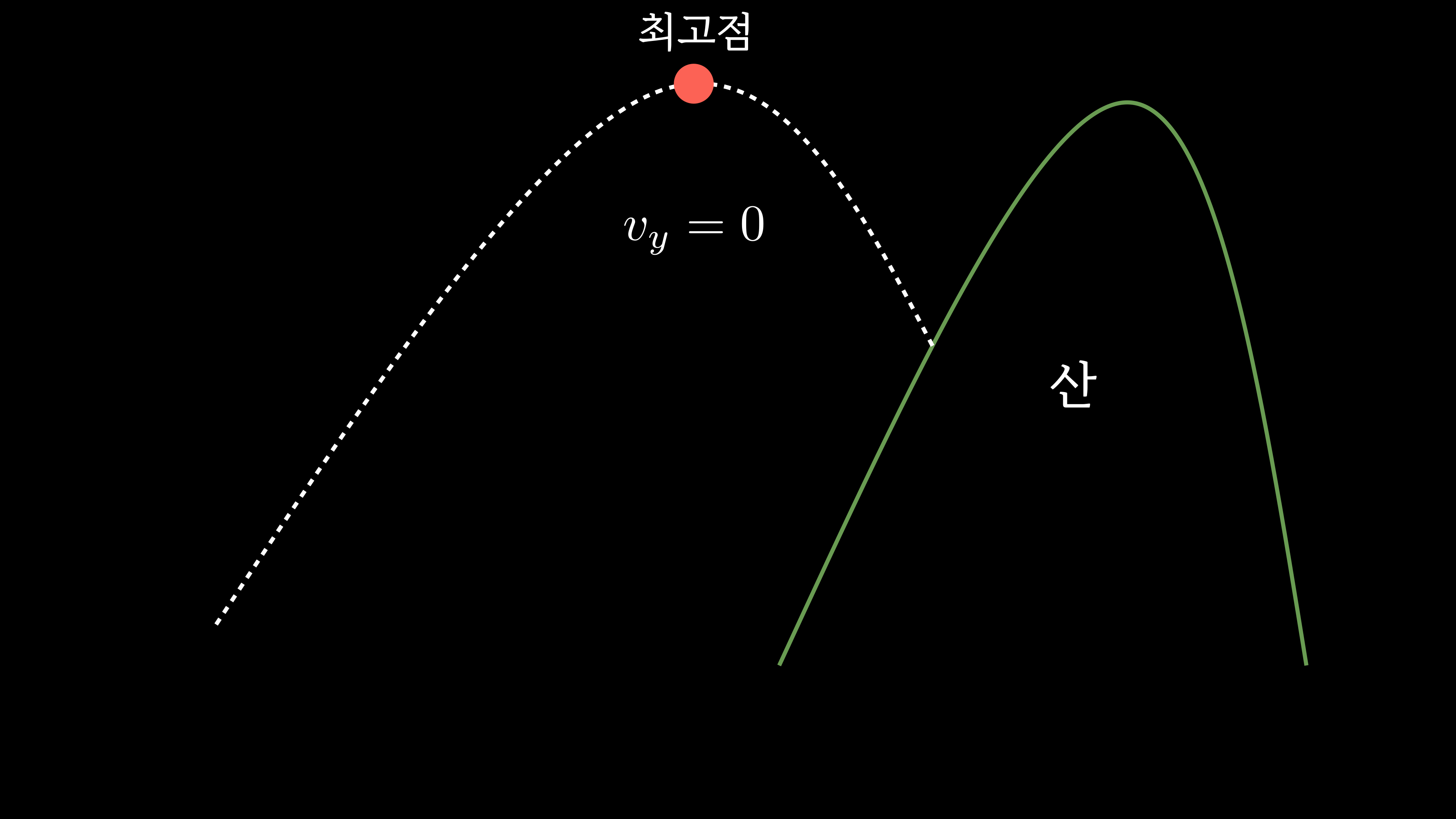
최고점에서 속도의 y성분은 0이 됩니다.
그래서 속도의 x성분이 곧 포물체의 속도가 됩니다.
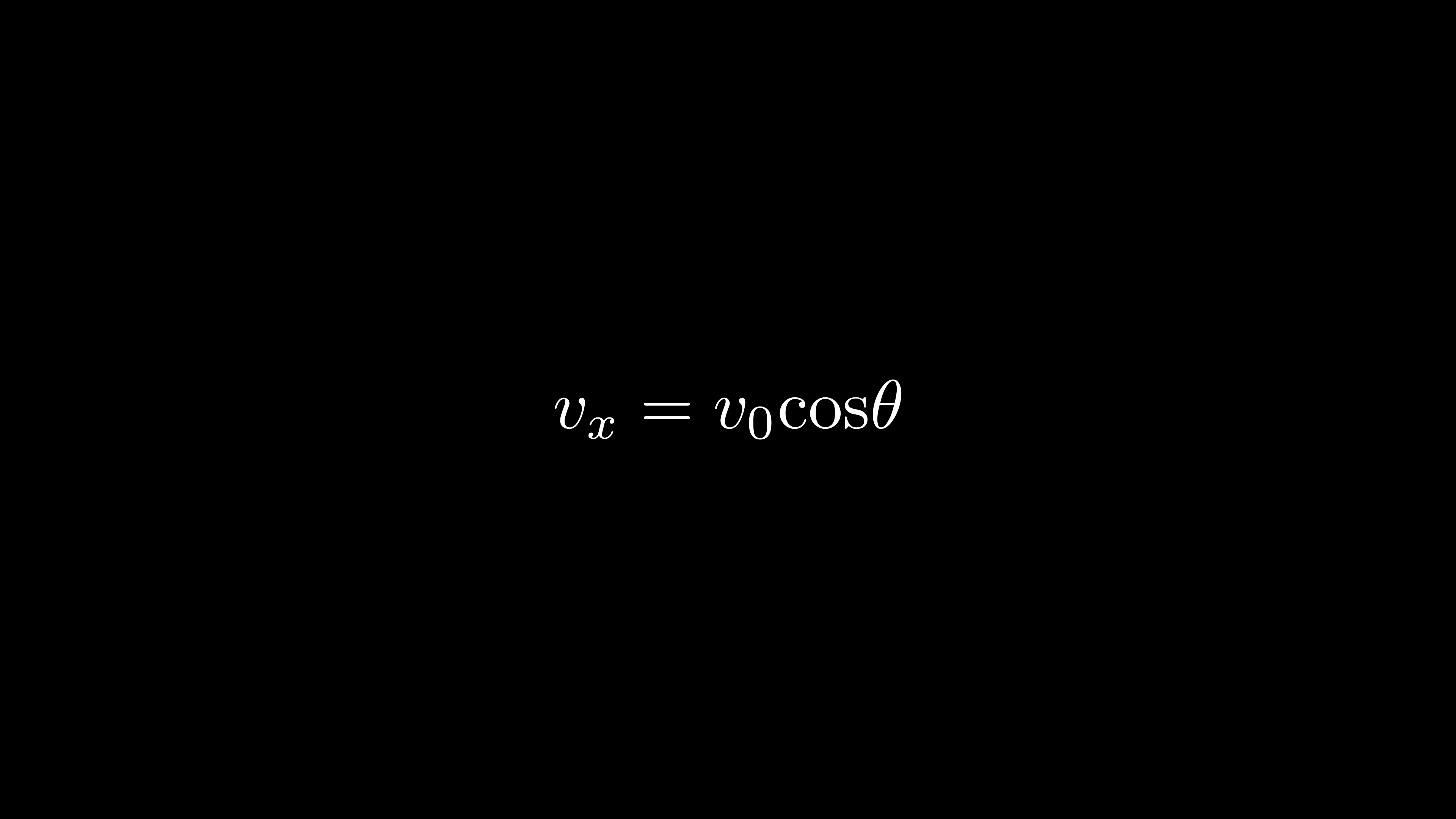
속도의 x성분은 초기속도에 cos(투사각)을 곱하면
쉽게 구할수 있습니다.
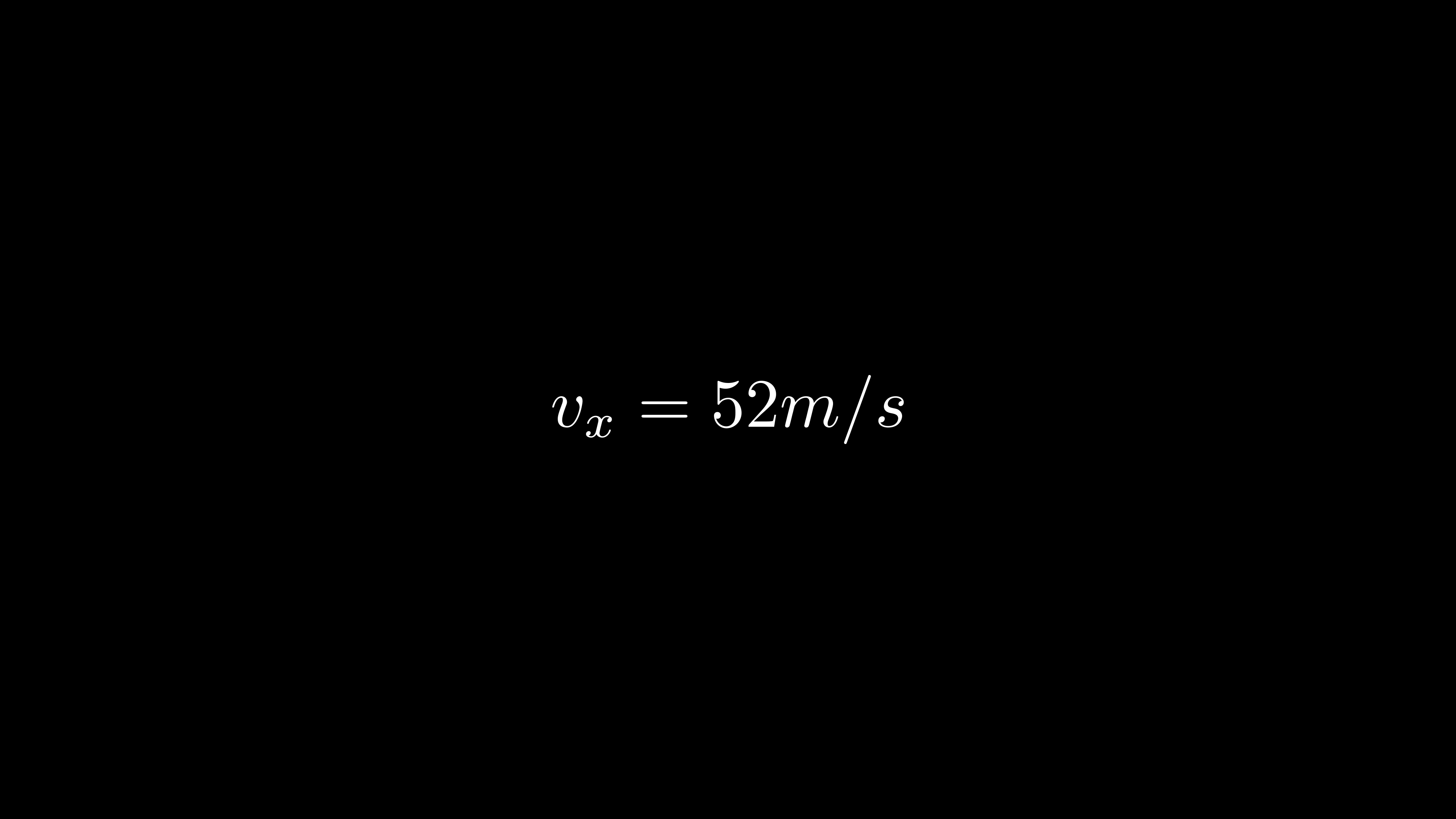
최고점에서 속도의 x성분은 52m/s가 됩니다.
따라서 (a)문제의 답은 52m/s입니다.
이제 (b)번 문제를 풀어보겠습니다.
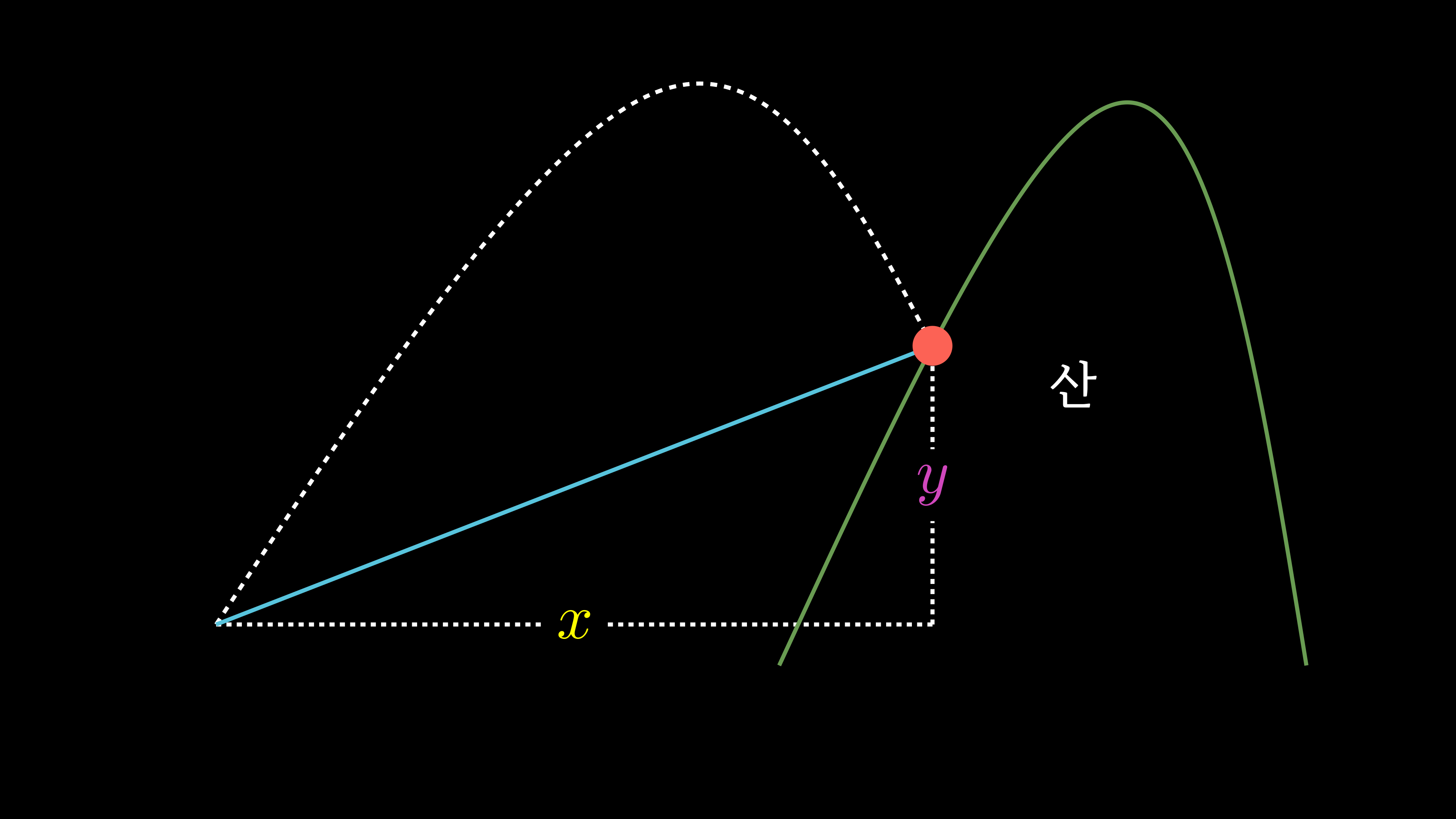
여기서 파란선이 발사된 곳에서 표적지 까지의
직선거리를 표시한 것입니다.
이때 파란선의 x성분(수평거리)과
y성분(수직거리)을 구할 수 있다면 파란선의
값을 구할 수 있습니다.
최종 도착지에 도착하는데
걸린 시간이 4초라는 것을 알고 있기 때문에
이 값을 공식에 대입해주면 수평거리 x의 값을
구할 수 있습니다.
x = 208m입니다.
그렇다면 수직거리 y는 어떤 값을 가질까요?
y값 (수직거리)을 구하는
공식에 t, g, v0, 각도 값을
대입해주면 y값 역시 구할 수 있습니다.
따라서 y = 43.6m가 됩니다.
이제 x, y값을 모두 구했으니
발사지점에서 표적지까지
포물체가 날아간 직선거리를 구할수 있습니다.
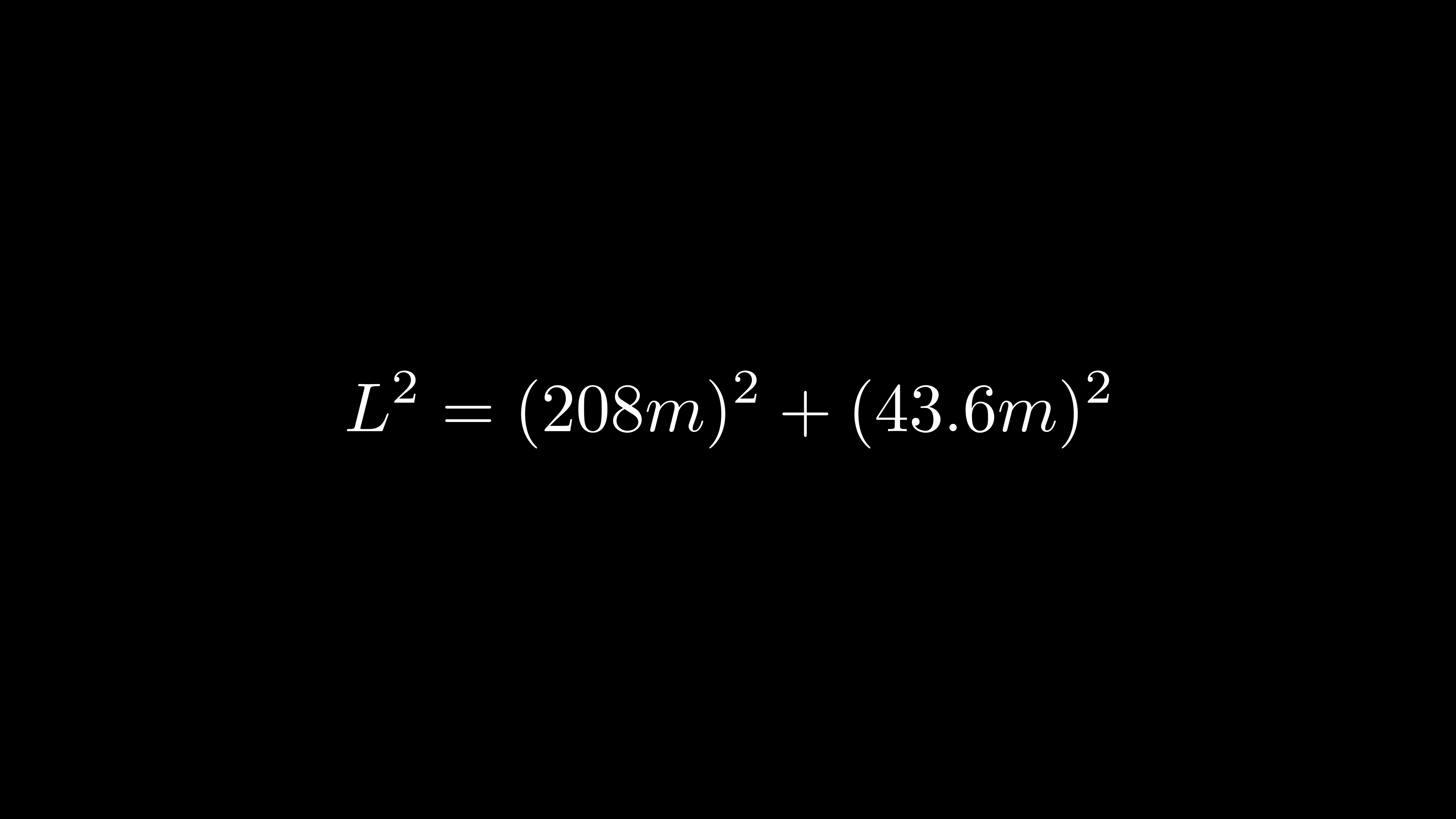
피타고라스 정리를 이용해서
수평거리의 제곱과 수직거리의 제곱의 합으로
거리의 제곱값을 구해줍니다.

그래서 포물체가 발사된 지점에서
산중턱에 머문 지점까지의 직선거리는
212m가 됩니다.
따라서 (a)의 정답은 52m/s (정확하게는 51.9xxx 유효숫자에 유의)
(b)의 정답은 212m(a와 마찬가지 유효숫자에 유의)가 됩니다.
결론
오늘은 이차원 운동에서 포물선 운동의 속도, 거리, 최고점 등 포물선 운동이 가지는 운동 특성을 통해 최고점에서의 속도와 최종 도착지까지의 거리를 알아볼 수 있는 문제를 풀어보았습니다. 여기서 중요한 부분은 이차원 운동이라는 개념 안에서 속도와 거리같은 벡터 물리량들은 x, y등 두 차원의 성분으로 나누어서 생각해볼 수 있다는 점입니다. 그래서 운동에 대해 보다 더 정밀하고 정량적인 예측과 분석이 가능하다는 점을 배웠다고 생각합니다.
부족한 글 읽어주셔서
감사합니다.
다음 포스팅으로 찾아 뵙겠습니다.

'일반물리학 문제풀이' 카테고리의 다른 글
| 일반물리학 문제풀이(일차원 운동 - 속도)2 (0) | 2023.05.20 |
|---|---|
| 일반물리학 문제풀이(일차원 운동 - 속도) (0) | 2023.05.20 |
| 일반물리학 문제풀이(에너지) (0) | 2023.05.18 |
| 일반물리학 문제풀이 (어림과 크기 정도 계산) (0) | 2023.05.16 |
| 일반물리학 문제풀이 (일차원 등가속도 운동) (0) | 2023.04.30 |







댓글 영역